换个姿势学C语言第5章5.2

换个姿势学C语言第5章获取完整的牌价数据 5.2节处理数组中的数据

0. 说明

《换个姿势学C语言》由何旭辉著，清华大学出版社2022年出版。感谢何老师！

这是一本非常不错的书！

第一、二、三章总结参考换个姿势学C语言第1-3章
第四章总结参考换个姿势学C语言第4章
第五章5.1节总结参考换个姿势学C语言第5章 5.1节
第五章5.2节总结参考换个姿势学C语言第5章 5.2节
第五章5.3节总结参考换个姿势学C语言第5章 5.3节

5. 获取完整的牌价数据

5.2 处理数组中的数据

数组可以用于存储多个同类型的数值，而对数组中的数据进行处理是程序员经常要进行的工作。

接下来我们需要处理的事情包括：

查找数组中的最大值；
数组排序。

这些任务看上去与外汇牌价显示无关，但我们将通过它们学习一些基础的概念。这些概念和技能在外汇牌价显示中均需用到。

5.2.1 查找数组中的最大值

要查找数组中元素的最大值，最简单的方式是从数组的第1个元素开始，依次寻找并“记住”最大值。这种方式效率很低，但对于未经排序的数组来说的确没有更好的方式，好在计算机的速度远远快于人类，因此这种方式也不是不能接受。

5.2.1.1 使用循环在数组中查找最大值

查找数组data[5] = { 61, 72, 23, 96, -70 };中的最大值，像下面编写代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
##include <stdio.h>
int main()
{
    int data[5] = { 61, 72, 23, 96, -70 };
    int max = data[0];
    for (int i = 1; i < sizeof(data) / sizeof(int); i++) {
        if (max < data[i]) {
            max = data[i];
        }
    }
    printf("数组中的最大值是: %d\n", max);
}

运行结果如下：

1
数组中的最大值是: 96

这是一个很简单的程序，但是在数组中查找最大值、最小值是常用的操作，我们可以把它们设置成函数，这样就可以对不同的数组进行查找了。

5.2.1.2 将查找最大值的函数写成自定义函数

将常用的操作定义成函数是程序员经常做的事，这可以大大提高未来编程的效率。
经验丰富的程序员往往会积攒自己的函数库。

在自定义最大值函数时，需要考虑如下问题：

函数的功能是什么？
- 在整型数组中查找最大值第1次出现的位置（索引值）。返回最大值在数组中的位置，而不是直接返回最大值本身的好处是，函数的调用者可能需要对数组进行进一步的处理（例如，改变它的值）。如果调用者还需要最大值本身，通过索引值也可以很方便获取。
函数的名字是什么？
- 函数的名字应该充分说明其功能和特性，考虑采用的函数名是findIndexOfMaxInIntArray，即在整型数组中查找最大值的索引。
函数需要传入哪些参数？
- 在数组中查找最大值，当然应该将数组传递给函数中。
函数是否需要返回值？返回何种类型的值？
- 函数要返回是索引值（下标），函数的返回值类型是int。

那么如何向函数传递数组？

在C语言中，无法向函数传递整个数组，只能向函数分别传递数组的起始地址和数组元素数据，这样设计违背直觉但可以提高程序的灵活性。

如何获取数组的首地址呢？可以使用&运算符，也可以直接用数组名来表示数组的首地址。

请看如下示例：

1
2
3
4
5
6
7
##include <stdio.h>
int main()
{
    int data[5] = { 61, 72, 23, 96, -70 };
    int* ptr_1 = data;
    printf("指针变量ptr_1的值是: %p\n", ptr_1);
}

运行结果如下：

1
指针变量ptr_1的值是: 00CFF738

可以看到，获取到了数据的首地址。

只有数组首地址是不够的，还需要传入数组的元素数量，元素数量是一个整型值，现在我们就可以确认函数的原型了，第1个参数int* array表示要传入数组的地址，第2个参数size用于表示数组的元素数量。

1
findIndexOfMaxInIntArray(int* array, int size);

然后，对函数进行封闭，并重新计算数组的最大值：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
##include <stdio.h>

int findIndexOfMaxInIntArray(int* array, int size)
{
    int max_value = array[0];
    int max_index = 0;
    for (int i = 0; i < size; i++) {
        if (array[i] > max_value) {
            max_value = array[i];
            max_index = i;
        }
    }
    printf("最大值的索引值为: %d\n", max_index);

    return max_index;
}

int main()
{
    int data[5] = { 61, 72, 23, 96, -70 };
    int maxindex = findIndexOfMaxInIntArray(data, sizeof(data) / sizeof(int));
    printf("数组中的最大值是: %d\n", data[maxindex]);
}

运行结果如下：

1
2
最大值的索引值为: 3
数组中的最大值是: 96

可以看到，一样的获取到了最大值。

上述程序存在一个问题，如果findIndexOfMaxInIntArray函数不小心对array数组的数据进行了修改，最终得到的结果可以不是我们想要的。看如下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
##include <stdio.h>

int findIndexOfMaxInIntArray(int* array, int size)
{
    int max_value = array[0];
    int max_index = 0;
    // 函数不小心对array数据进行了变更
    array[1] = 100;
    for (int i = 0; i < size; i++) {
        if (array[i] > max_value) {
            max_value = array[i];
            max_index = i;
        }
    }
    printf("最大值的索引值为: %d\n", max_index);

    return max_index;
}

int main()
{
    int data[5] = { 61, 72, 23, 96, -70 };
    int maxindex = findIndexOfMaxInIntArray(data, sizeof(data) / sizeof(int));
    printf("数组中的最大值是: %d\n", data[maxindex]);
    for (int i = 0; i < sizeof(data) / sizeof(int); i++) {
        printf("data[%d] = %d\n", i, data[i]);
    }
}

运行结果如下：

1
2
3
4
5
6
7
最大值的索引值为: 1
数组中的最大值是: 100
data[0] = 61
data[1] = 100
data[2] = 23
data[3] = 96
data[4] = -70

此时查找到的数组最大值的索引值变成了1，而不是之前的3，说明自定义函数内部已经将数组data的数据变更了，这可能给程序带来严重的错误。

因此，在函数定义时，要对传入的数组进行保护。

5.2.1.3 使用const限定符保护数组中的数据

在C语言中提供了保护数组的方式——在指针参数前面加上const限定符。像下面这样：

1
int findIndexOfMaxInIntArray(const int* array, int size);

通过在参数int* array前面加上限定符const，向编译器明确说明了：不允许在函数内部修改指针array指向的内存值。

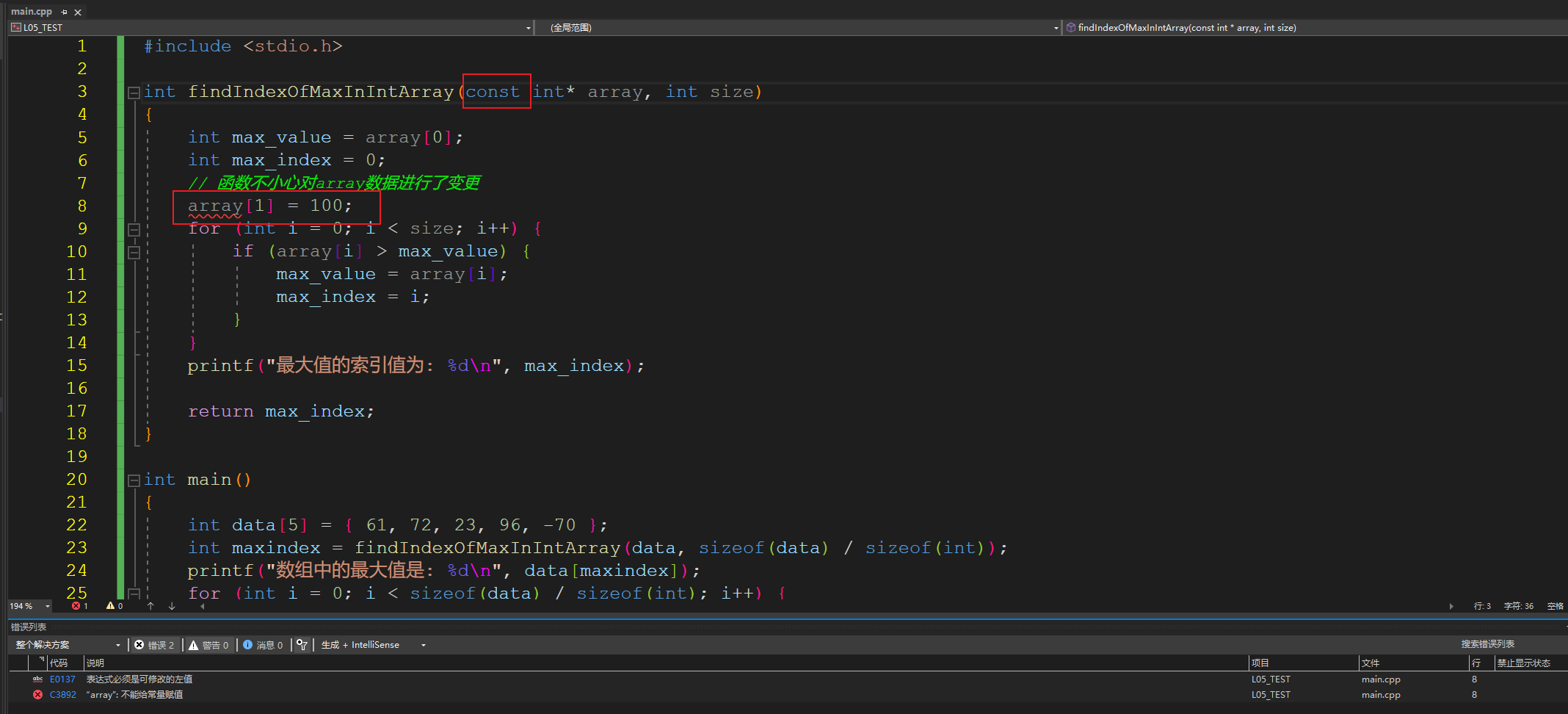
加上const限定符后，再编译就会报以上异常。这样就不用担心函数内部会不小心修改了数组的内容！！！

将异常代码删除掉：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
##include <stdio.h>

int findIndexOfMaxInIntArray(const int* array, int size)
{
    int max_value = array[0];
    int max_index = 0;
    for (int i = 0; i < size; i++) {
        if (array[i] > max_value) {
            max_value = array[i];
            max_index = i;
        }
    }
    printf("最大值的索引值为: %d\n", max_index);

    return max_index;
}

int main()
{
    int data[5] = { 61, 72, 23, 96, -70 };
    int maxindex = findIndexOfMaxInIntArray(data, sizeof(data) / sizeof(int));
    printf("数组中的最大值是: %d\n", data[maxindex]);
    for (int i = 0; i < sizeof(data) / sizeof(int); i++) {
        printf("data[%d] = %d\n", i, data[i]);
    }
}

然后再执行程序，运行结果如下：

1
2
3
4
5
6
7
最大值的索引值为: 3
数组中的最大值是: 96
data[0] = 61
data[1] = 72
data[2] = 23
data[3] = 96
data[4] = -70

可以看到又能正常获取最大值了。

同理，再增加一个获取数组最小值的索引值的函数：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
##include <stdio.h>

int findIndexOfMaxInIntArray(const int* array, int size)
{
    int max_value = array[0];
    int max_index = 0;
    for (int i = 0; i < size; i++) {
        if (array[i] > max_value) {
            max_value = array[i];
            max_index = i;
        }
    }
    printf("最大值的索引值为: %d\n", max_index);

    return max_index;
}

int findIndexOfMinInIntArray(const int* array, int size)
{
    int min_value = array[0];
    int min_index = 0;
    for (int i = 0; i < size; i++) {
        if (array[i] < min_value) {
            min_value = array[i];
            min_index = i;
        }
    }
    printf("最小值的索引值为: %d\n", min_index);

    return min_index;
}

int main()
{
    int data[5] = { 61, 72, 23, 96, -70 };
    int maxindex = findIndexOfMaxInIntArray(data, sizeof(data) / sizeof(int));
    printf("数组中的最大值是: %d\n", data[maxindex]);
    int minindex = findIndexOfMinInIntArray(data, sizeof(data) / sizeof(int));
    printf("数组中的最小值是: %d\n", data[minindex]);
    for (int i = 0; i < sizeof(data) / sizeof(int); i++) {
        printf("data[%d] = %d\n", i, data[i]);
    }
}

然后再执行程序，运行结果如下：

1
2
3
4
5
6
7
8
9
最大值的索引值为: 3
数组中的最大值是: 96
最小值的索引值为: 4
数组中的最小值是: -70
data[0] = 61
data[1] = 72
data[2] = 23
data[3] = 96
data[4] = -70

5.2.2 数组排序

对数组中的数值进行排序也是经常进行的操作，排序是将多个数据按照特定的规则进行排序，最常用到的排序规则是对数字进行数值排序。
对字符或字符串则是字典顺序（以字母或汉字在编码表中的顺序）。
排序虽然是一个简单的问题，但排序算法却有很多种，这些排序算法的实现方法、适用场景、性能各不一样。虽然大部分人认为排序是一个已经解决的问题，但是新的、有用的算法仍然在不断地被发明。
比较常用的数组排序方法有冒泡排序、插入排序、选择排序、快速排序等。

5.2.2.1 选择排序的基本原理

我们使用选择排序来对数组进行排序。

选择排序的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置；然后，再从剩下的、未排序的元素中继续寻找最小（大）元素；然后把找到的元素放到已排序序列的末尾。以此类推，直到所有的元素排序完毕。

假如我们还是对之前的int data[5] = { 61, 72, 23, 96, -70 };这个数组进行排序。

下面手动来一次演练，从小到大排序。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
## 原始值
61, 72, 23, 96, -70

## 第一轮查找
## 将第1个元素与第2个元素对比，61 < 72,位置保持不变
+---+
|   |
61, 72, 23, 96, -70
## 第一轮查找
## 将第1个元素与第3个元素对比，61 > 23,需要交换位置
+-------+
|       |
61, 72, 23, 96, -70
## 交换后元素如下
+-------+
|       |
23, 72, 61, 96, -70
## 第一轮查找
## 将第1个元素与第4个元素对比，23 < 96,位置保持不变
+-----------+
|           |
23, 72, 61, 96, -70
## 第一轮查找
## 将第1个元素与第5个元素对比，23 > -70,需要交换位置
+----------------+
|                |
23, 72, 61, 96, -70
## 交换后元素如下
+----------------+
|                |
-70, 72, 61, 96, 23

## 第1轮查找完后，找到最小元素为-70
#####################################################

## 再进行第2轮查找
## 将第2个元素与第3个元素对比，61 < 72,需要交换位置
     +---+
     |   |
-70, 72, 61, 96, 23
## 交换后元素如下
     +---+
     |   |
-70, 61, 72, 96, 23
## 将第2个元素与第4个元素对比，61 < 96,位置保持不变
     +-------+
     |       |
-70, 61, 72, 96, 23
## 将第2个元素与第5个元素对比，61 > 23,需要交换位置
     +-----------+
     |           |
-70, 61, 72, 96, 23
## 交换后元素如下
     +-----------+
     |           |
-70, 23, 72, 96, 61

## 第2轮查找完后，找到最小两个元素为-70、23
#####################################################

## 再进行第3轮查找
## 将第3个元素与第4个元素对比，72 < 96,位置保持不变
         +---+
         |   |
-70, 23, 72, 96, 61
## 将第3个元素与第5个元素对比，72 > 61,需要交换位置
         +-------+
         |       |
-70, 23, 72, 96, 61
## 交换后元素如下
         +-------+
         |       |
-70, 23, 61, 96, 72

## 第3轮查找完后，找到最小三个元素为-70、23、61
#####################################################

## 再进行第4轮查找
## 将第4个元素与第5个元素对比，96 > 72,需要交换位置
             +---+
             |   |
-70, 23, 61, 96, 72
## 交换后元素如下
             +---+
             |   |
-70, 23, 61, 72, 96
## 第4轮查找完后，找到最小四个元素为-70、23、61、72
#####################################################

## 最后未排序的元素只剩下96了，这个是最大值，不需要再排序了
## 因此，最终排序好的顺序是
-70, 23, 61, 72, 96

5.2.2.2 交换两个元素

交换两个元素是经常遇到的事情，可以将其编写成函数。

如下所示代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
##include <stdio.h>

// 交换x和y的值
void swapInt(int* x, int* y)
{
    int temp = *x;
    *x = *y;
    *y = temp;
}

int main()
{
    int x = 1;
    int y = 2;
    printf("x=%d y=%d\n", x, y);
    // &是一个运算符，用于取得变量的首地址
    swapInt(&x, &y);
    printf("x=%d y=%d\n", x, y);
}

运行代码，输出结果如下：

1
2
x=1 y=2
x=2 y=1

可以看到，x和y的值已经互换了。

进行排序：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
##include <stdio.h>

// 交换x和y的值
void swapInt(int* x, int* y)
{
    int temp = *x;
    *x = *y;
    *y = temp;
}

// 打印数组元素
void printArray(const int* array, int size)
{
    for (int i = 0; i < size; i++) {
        printf("%d ", array[i]);
    }
    printf("\n");
}

// 使用选择排序对数组进行排序
void selectSort(int* array, int size)
{
    for (int i = 0; i < size; i++) {
        for (int j = i + 1; j < size; j++) {
            if (array[j] < array[i]) {
                swapInt(&array[i], &array[j]);
            }
        }
        //printArray(array, size);
    }
}

int main()
{
    int data[5] = { 61, 72, 23, 96, -70 };
    int size = sizeof(data) / sizeof(int);
    printArray(data, size);
    selectSort(data, size);
    printArray(data, size);
}

然后再执行程序，运行结果如下：

1
2
61 72 23 96 -70
-70 23 61 72 96

可以看到，数组已经正常排序了。

下面是加了控制排序的方式的标志的代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
##include <stdio.h>

// 交换x和y的值
void swapInt(int* x, int* y)
{
    int temp = *x;
    *x = *y;
    *y = temp;
}

// 打印数组元素
void printArray(const int* array, int size)
{
    for (int i = 0; i < size; i++) {
        printf("%d ", array[i]);
    }
    printf("\n");
}

// 使用选择排序对数组进行排序
// array 需要排序的数组
// size 数组的长度
// flag 排序标志，1升序，0降序
void selectSort(int* array, int size, int flag)
{
    for (int i = 0; i < size; i++) {
        for (int j = i + 1; j < size; j++) {
            if (flag > 0) {
                // 升序
                if (array[j] < array[i]) {
                    swapInt(&array[i], &array[j]);
                }
            } else {
                // 降序
                if (array[j] > array[i]) {
                    swapInt(&array[i], &array[j]);
                }
            }
        }
        //printArray(array, size);
    }
}

int main()
{
    int data[5] = { 61, 72, 23, 96, -70 };
    int size = sizeof(data) / sizeof(int);
    printArray(data, size);
    selectSort(data, size, 1);
    printArray(data, size);
    selectSort(data, size, 0);
    printArray(data, size);
}

然后再执行程序，运行结果如下：

1
2
3
61 72 23 96 -70
-70 23 61 72 96
96 72 61 23 -70

通过给selectSort函数第三个参数传参，当flag值为1时，升序排序；当flag值为0时，降序排序。注意，此处并没有详细对flag进行限定。

换个姿势学C语言 第5章 获取完整的牌价数据 5.2节 处理数组中的数据

0. 说明

5. 获取完整的牌价数据

5.2 处理数组中的数据

5.2.1 查找数组中的最大值

5.2.1.1 使用循环在数组中查找最大值

5.2.1.2 将查找最大值的函数写成自定义函数

5.2.1.3 使用const限定符保护数组中的数据

5.2.2 数组排序

5.2.2.1 选择排序的基本原理

5.2.2.2 交换两个元素

换个姿势学C语言第5章获取完整的牌价数据 5.2节处理数组中的数据